In-depth view; how to calculate whether your forklift can handle certain goods.

Counterbalance forklifts are the most commonly used type of forklifts in warehouses, construction sites, and various industrial environments. But what keeps them stable while lifting heavy loads? The answer lies in a fundamental concept from physics called the principle of moments. Understanding how this principle works can shed light on the design and operation of these powerful machines.

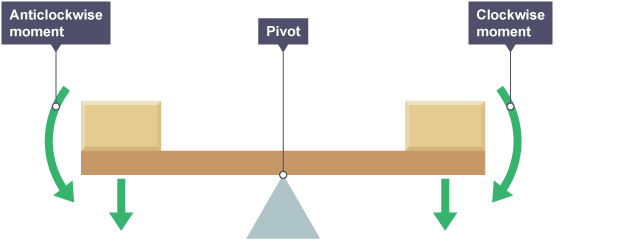
The Basics of the Principle of Moments

The principle of moments states that for an object to remain in equilibrium (or balanced), the total clockwise moments around a pivot must equal the total counterclockwise moments. In the case of a counterbalance forklift, the "pivot" point is the front axle, around which the forces balance to keep the forklift stable.

How the Principle of Moments Keeps Forklifts Stable

Counterbalance forklifts are designed to carry loads in front of the machine, with the weight of the load creating a clockwise moment around the front axle. To prevent tipping forward, forklifts are equipped with a heavy counterweight located at the rear of the machine, creating a counterclockwise moment that balances the load. Here’s how these elements work together:

1. Load and Moment Creation: When a forklift picks up a load, the weight of the load acts at a distance from the front axle, generating a clockwise turning force, or moment. This moment depends on:

   • The weight of the load.

   • The distance from the load’s center of gravity to the front axle (known as the load center).

2. Counterweight and Balance: To balance the clockwise moment, the forklift uses a counterweight at the back of the vehicle. This counterweight creates a counterclockwise moment that counters the tipping force caused by the load. The heavier the load or the farther it is from the front axle, the greater the counterweight needs to be to keep the forklift stable.

3. Calculating Stability with the Principle of Moments:

   • Clockwise Moment (due to the load) = Load Weight × Load Center Distance

   • Counterclockwise Moment (due to the counterweight) = Counterweight × Distance from Counterweight to Front Axle

   For stability, the counterclockwise moment needs to be equal to or greater than the clockwise moment created by the load. If the load is too heavy or positioned too far forward, the forklift may lose balance, potentially tipping forward.

4. Using our calculator; https://www.rsmech.org/calculator you can input the values to check if the goods can be lifted safely, else if you are more handy with a calculator. The formula is as follows

   Forklift Rated Tonnage X Forklift Rated Load Centre = Goods Tonnage X Goods Centre of Gravity Distance from Fork Face

   
   

So you might ask how do we calculate an object's centre of mass? If your goods are palletised or uniformed in its mass distribution it is easier to determine it's centre of mass. Calculating an object’s center of gravity is essential for understanding how it will balance or behave when lifted or rotated. The center of gravity (CoG) is the point where an object's weight is evenly distributed in all directions. For simple shapes, the center of gravity can often be calculated mathematically, while for irregular shapes, it may require a bit more work. Here’s a guide on how to calculate it:

1. For Simple, Symmetrical Shapes

For regular, symmetrical shapes like a rectangle, square, or cylinder, the center of gravity is often in the geometric center.

• Rectangle or Square: The CoG is at the intersection of the diagonals, which is the center point of the shape.

• Circle or Cylinder: The CoG is at the midpoint along the diameter (for a circle) or the central axis (for a cylinder).

• Uniform Rod or Beam: The CoG is located at the midpoint of the length of the rod.

In these cases, the center of gravity is easy to find because it lies in the geometric center.

2. For Combined Shapes

If an object is made up of several symmetrical shapes, you can find the center of gravity by calculating the weighted average of each shape’s center of gravity.

• Step 1: Divide the object into simpler shapes (e.g., rectangles, circles).

• Step 2: Find the area or volume and center of gravity of each simple shape.

• Step 3: Use the formula for the center of gravity (CoG) in each direction (x, y, and sometimes z):

  

  where:

  • xix_ixi​ and yiy_iyi​ are the coordinates of each shape’s center of gravity.

  • wiw_iwi​ is the weight or area of each shape.

• Step 4: Combine these coordinates to get the overall center of gravity.

3. For Irregular Objects

For objects without symmetrical shapes, such as machinery or complex designs, finding the CoG may require more detailed methods:

• Suspension Method: Suspend the object from different points and let it hang freely. Draw a vertical line downwards from each suspension point. The intersection of these lines is the center of gravity.

• Moment Method (for practical applications like machinery): When an object’s weight distribution varies widely, calculate the center of gravity by breaking it down into smaller sections, assigning each section a weight and location. Using the formula for combined shapes (from Step 2), determine the overall center of gravity.

4. Example Calculation

Let’s say you have an L-shaped object made from two rectangles, A and B, with weights and centers of gravity already known:

• Rectangle A: Weight = 10 kg, CoG at (2, 3)

• Rectangle B: Weight = 15 kg, CoG at (5, 6)

The combined center of gravity can be calculated as:

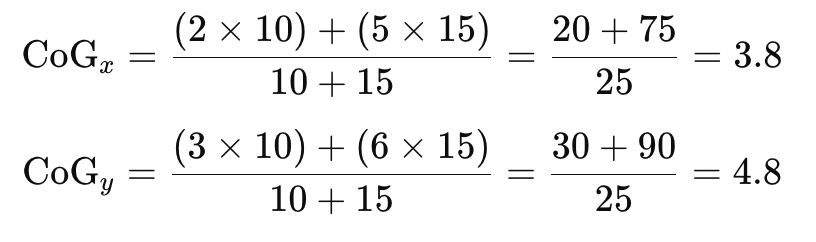
So, the center of gravity of the L-shaped object is at (3.8, 4.8).

Summary

Finding the center of gravity depends on the shape:

• Symmetrical shapes: Use the geometric center.

• Combined shapes: Calculate the weighted average of each shape's center.

• Irregular shapes: Use suspension or break it into smaller sections to approximate.